Is composition of functions associative?

April 1, 2012July 31, 2021Joel

See also a version of this post on Blogger at https://explaining-maths.blogspot.com/2021/07/composition-of-functions-is-associative.html (using MathJax) where the maths looks a bit clearer.

Well, of course it is.

[Notes in italics added 30/7/12: In spite of the date of this post, it is not intended to be a joke (except in as much as my concerns here may appear amusing!). However, the title of the post might be somewhat misleading. I am not suggesting that there is actually any doubt about the truth of these standard results, namely that composition of functions is associative, and that evaluation of expressions with nested brackets is unambiguous. What I am really asking is whether the standard proof of the fact that composition of functions is associative is a fully convincing one.]

I’m sure you have seen the standard proof that composition of functions is associative, but let me remind you how it goes.

Let $W,X,Y$ and $Z$ be sets, and suppose that we are given functions

$h:W \to X$ , $g:X \to Y$ and $f:Y \to Z$

We show that $(f \circ g) \circ h = f \circ (g \circ h)$ as follows.

Let $w \in W$ . Then

$((f \circ g) \circ h)(w) = (f \circ g)(h(w)) = f(g(h(w)))$

and

$(f \circ (g \circ h))(w) = f( (g\circ h)(w)) = f(g(h(w)))$ .

Since $((f \circ g) \circ h)(w) = (f \circ (g \circ h))(w)$

for all $w\in W$ , we have

$(f \circ g) \circ h = f \circ (g \circ h)\,.$

Now perhaps it is just me, but I suspect that seeing so many brackets around here might make for some initial confusion for the students. But is there more to it than that? As mathematicians, we know how to evaluate expressions involving lots of brackets. In fact we all learned how to prioritize brackets over the other mathematical operations when we were at school. But somewhere implicit in this is a confidence that we know how to evaluate expressions involving nested brackets and that these expressions are unambiguous.

But how do we know that evaluating expressions with nested brackets is unambiguous? Are we assuming here that composition of functions is associative? [Or maybe we need, at some earlier stage, to perform a check that is essentially equivalent to proving that composition of functions is associative?] That would then lead to circularity in the argument above. [Or at least it might render the standard proof less satisfactory?]

Here is my suggestion for breaking out of this possible problem.

First of all, how else could we define the function $f\circ g$ . Perhaps we are happy at least with the definition $(f \circ g)(x) = f(g(x))$ : after all, there doesn’t seem to be any ambiguity there. Still, let’s see this another way.

Given $x \in X$ , set $y = g(x) \in Y$ , and then set $z = f(y) \in Z$ . Then the function $f \circ g$ is the function $x \mapsto z$ , where $z$ is defined in terms of $x$ as above.

How can this possibly help? Well, if we return to the composition of functions, let’s see what the new definitions of

$(f \circ g) \circ h$ and $f \circ (g \circ h)$

look like.

Let $w \in W$ . Set $x=h(w) \in X$ , set $y=g(x) \in Y$ and set $z=f(y) \in Z$ .

Examining our definitions above, we discover that

$z= (f \circ g)(x)$ where $x=h(w)$ , and so

$z = ((f\circ g)\circ h)(w)$

(and you could rewrite this in longhand in English if you want to avoid some of the brackets round the functions!)

Similarly

$y = (g\circ h)(w)$ and $z = f(y)$ , giving us

$z= (f \circ (g\circ h))(w)$

(and again, we can rewrite everything in English to avoid some of the brackets round the functions).

The rest of the proof is as before.

I’m not really sure whether this helps, or hinders in general! But perhaps there are a few more people like me out there who might be glad to see that there isn’t really any circularity in the proof after all. That is, if I haven’t introduced some new problems above …

[Feedback so far suggests that I may be in a minority of one with my concerns about the standard proof!]

Pingback: Composition of Functions is Associative | New Math Done Right
Toby Bailey July 29, 2012 / 8:42 am

There is no question of associativity in interpreting an expression formed from brackets, and therefore, as far as I can see no possibility of circularity.

More to the point, *if* you seriously think that there is something to say about interpreting multiply bracketed expressions that your students do not already know, then surely you need to say it far earlier since this can hardly be the only place that they occur. Indeed, a similar complication of brackets is easily obtained in basic algebra.

LikeLike

Reply
- Toby Bailey July 29, 2012 / 8:44 am
  
  Just noticed the date of posting of the original article. As a joke, it’s a bit too similar to a lot of maths teaching.
  
  LikeLike
  
  Reply
Joel July 29, 2012 / 8:54 am

Toby, it wasn’t a joke.
It was a personal response to the issue, and one which made me feel a bit happier about it! Some might find my comments helpful, others irrelevant.
Let me ask: why do you think that there is no issue involved in evaluating nested brackets? I don’t claim to have resolved that issue here, except perhaps in the very special case which corresponds to function composition. Presumably the general case is discussed elsewhere?
Joel

LikeLike

Reply
- Toby Bailey August 5, 2012 / 8:38 am
  
  I still don’t see what you are worrying about. Brackets are a means of writing unambiguous instructions to carry out multiple binary operations (or function evaluations of course). Associativity is about whether two different bracketed expressions are in fact equal as a consequence of the properties of the particular binary operation. There is not even the scope for circularity.
  
  I quite see that there is an issue to think about as to whether bracketed expressions do define a calculation to be done unambiguously, and doubtless somebody has written on this although it strikes me as obvious that they do. And, as I said before, if we are in any doubt about this then we should sort it out far earlier since it would affect every reasonably complicated calculation we ever do.
  
  I certainly have not experienced a failure to understand brackets as being an issue with UG maths teaching – although of course they are often used (or more often, not used) rather carelessly.
  
  But students will certainly find the associativity of function composition statement and proof difficult, but not, I would claim, because of imagining an ambiguity with brackets. I would suggest that the issue is probably in understanding the statement and the need for a proof. On the first, we are probably dealing with what has often been referred to as a “process-object” difficulty: the huge cognitive step from thinking of a given function as a process to be applied to an argument to thinking of a function as an object itself to which operations can be applied. One sees this at a more elementary level when students have difficulty reasoning about an abstract function about which only some properties are known, compared with a concrete one which can be evaluated on a calculator.
  
  Secondly, there is the related difficulty with students not realising that the “rules of algebra” change according to the properties of the objects and operations. Having dealt at High School almost entirely with numbers, they are inclined to think of a(bc)=(ab)c as an absolute truth of mathematics rather than as a law that may or may not hold. I only realised that this may be a related problem as I wrote this: I suspect that the process-object difficulty causes students to fall back on using the “usual rules of algebra” because they are not yet equipped with the necessary schema to work with the functions as objects.
  
  LikeLike
  
  Reply
  - Joel August 11, 2012 / 9:12 pm
    
    The mathematics required to explain what it actually means to evaluate a mathematical expression is standard enough, but involves an inductive construction which I suspect would be somewhat tricky for a typical first-year mathematics undergraduate. So I doubt that this would be covered rigorously before students have to meet composition of functions. That means that students are taking certain things on trust at this point.
    When you take standard facts on trust (like the fact that you can evaluate mathematical expressions unambiguously), you don’t necessarily know which results are used/assumed when people actually give rigorous proofs of those facts.
    What I hope my post does is to give a short cut for those who, like me, might otherwise need to look at the full details involved in the inductive construction, and check that there is no hidden use of the associativity of composition of functions there.
    I suspect that I am, and will remain, in a vanishingly small minority in having had any concerns at all! I have certainly never come across a student with this concern, and I may never meet one.
    
    LikeLike
Joel July 29, 2012 / 1:05 pm

Somewhat related to my concerns here is a more advanced fact.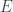
If a Banach space $E$ is reflexive then so is its topological dual $E^*$ .
Some of my students asked me whether the following argument was acceptable:

“Since $E$ is reflexive, identification allows us to write
$E = E^{**}$
and so, taking $*$ of both sides gives
$E^* = E^{***}\,,$
from which $E^*$ is also reflexive.”

That attempted argument is definitely dubious!
It is this type of concern that brought me back to wondering whether there is an issue.
Perhaps there really is nothing to it. If you are not worried then please feel free to ignore this post.
Part of the point of the post is to convince the rare concerned reader (someone like myself) that there really is no circularity after all here.

LikeLike

Reply
Neil March 27, 2013 / 9:09 pm

Hey. Thanks for the post. I was confusing myself with this today. It was one of those ‘I know this is stupid but something doesn’t feel right’ moments. I also thought I would be the only one with an issue but apparently not.

My confusion was also due to me wandering whether the fact that
fg(x) = f(g(x)) comes before or after associativity.

I’ve worked on it a bit and this is my present understanding. Which may be of some help. Take functions to be defined by their source, target and graph. Ie, ordered pairs with elements from given sets. Then this definition implies that composition is associative and it implies that fg(x) = f(g(x)). But now apparently fg(x) = f(g(x)) also implies associativity. Which is sort of weird:

Definition implies associative
Definition implies fg(x) = f(g(x))
fg(x) = f(g(x)) implies associativity

Maybe I should just reproduce the set theoretic proof of associativity. Which is:
(x,y) in f(gh)
= There exists z such that (x,z) in gh and (z,y) in f
= There exists z and w such that (x,w) in h and (w,z) in g and (z,y) in f
= There exists w and z such that (x,w) in h and (w,z) in g and (z,y) in f
= There exists w such that (x,w) in h and (w,y) in fg
= (x,y) in (fg)h

And the proof that fg(x) = f(g(x))

Recall that fg(x) is the unique element y such that (x,y) in fg. Or, formally stated:
{ fg(x) } = { y | (x,y) is in fg }
so then
{ fg(x) } = { y | There is a z | (x,z) is in g and (z,y) is in f }
But since { g(x) } = { y | (x,y) is in g }
we have { g(x) } = { z }
so z = g(x)
so { fg(x) } = { y | (x,g(x)) is in g and (g(x),y) is in f }
but again we find that if (g(x), y) is in f then y = f(g(x))
So { fg(x) } = { f(g(x))}
and finally fg(x) = f(g(x))

So really the question is how best to define function composition and how best to prove associativity. It seems we can keep both associativity and that fg(x) = f(g(x)) by dropping the set theoretic definition and just defining fg to be all pairs (x,f(g(x))). This will lose a lot in other places though. As for the proof: Is it possible that we can have and operation * on functions where f*g(x) =f(g(x)) but * is not associative? Seems the answer is no. Is it possible that we can have an operation * on functions such that * is associative but f*g(x) is not f(g(x))? We have not shown otherwise. (normal addition of functions an example?) How should we prove associativity? Personally I prefer the proof straight from the set theoretic definition. I don’t think you should use theorems where definitions and axioms will do.

)

LikeLike

Reply
- JoJoModding April 13, 2019 / 4:40 pm
  
  If someone still wonders about this: There is no circularity here. You need to get your definitions right.
  Let’s start by defining functions:
  A function f: A->B (A,B are sets) is an object which has one operation, called application. We can apply our function to every element of A and the result is exactly one fixed element of B, called f(x). So for applying f to an x we write f(x).
  
  Now we can define function composition. For two functions f: A->B and g: B->C, where A,B,C are sets, we define the function (f o g): A->C as the function for which (f o g)(x) = f(g(x)) for all x in A. It follows from the definitions here that the composition of two functions is unique.
  
  We can now prove that function composition is associative with the original proof from the answer.
  
  LikeLike
  
  Reply
Michele W July 14, 2014 / 3:16 pm

Joel –

This really helped me with something that I was doing. I needed to prove associativity of a particular mapping function, but the standard proof didn’t quite convince me. Nor did I like some of the other alternatives out there. I consider yours to be more rigorous than the others – you don’t take anything for granted, and you really proved everything. I’m so glad I came across your explanation here. Thanks so much!

LikeLike

Reply
Justin Benfield April 23, 2015 / 10:25 am

To the OP: You are right to be bothered that that supposed proof. It starts in the wrong place. What are trying to show is that

(f \circ g) \circ h = f \circ (g \circ h)

this means you must start with one of them and show that it is actually equal the other. This amounts to diagram chasing your way from an arbitrary z \in Z backwards through one of them to (a subset of) the domain W, and then forwards through the other back the arbitrary z you started with.
Technically, you need the z \in Z that you start with to be in the image of W for the correct composite, hence will need to do the diagram chasing twice, once in each direction, showing that the image under each composite of the pre-image of z under the other composite contains z, and from that conclude that both composites agree (and since z was arbitrary, this holds everywhere).
It’s a bit long and tedious, but honestly not that difficult of a proof.

LikeLike

Reply
- Justin Benfield April 23, 2015 / 8:08 pm
  
  I realized a few hours later that I was wrong with the above, to prove that two functions are identical, all that you need to show is that their domain and codomain are the same, and that for every element in their common domain, the image of that element is the same. In the present case of function composition, the common domain (using the OPs notation) is $ W $. their common codomain is $ Z $. Hence all we need to show is that for an arbitrary $ w \in W $, $ (f \circ g) \circ h = f \circ (g \circ h) $. I think it’s very important to point out that things such as $ g(y) $, and $ g(f(x)) $ are actually elements of, $ Z $, and $ Y $ respectively. The definition of function composition says that evaluating the composite (say, going from $x \in X $ to $ (f \circ g)(x) \in Z $) is the same as going from $ x \in X $ to $ f(x) \in Y by the ‘inside function’ then going from $ f(x) \in Y $ to $ g(f(x) \in Z) $.
  
  LikeLike
  
  Reply
shaun October 23, 2015 / 2:42 pm

finally I see this post and realized my concern were genuine. In most of the proofs they presumed the associativity rather than actually proving it!.thanks a lot.

LikeLike

Reply
Pingback: On indexing operators and composition – Mubashir Qasim
Pingback: On indexing operators and composition | Open Data Science
Galaxian January 23, 2019 / 3:36 am

That the monstrosities “g of h” and “f of g” are well-defined is assured by your having each function’s target set be contained within the source set of the next. Thank you so much for your nice blog posts. But we might contest the notions of one-to-one and many-to-one correspondence altogether: We take these ideas as sound on faith and (inductive) experience.

LikeLike

Reply